নবম শ্রেণীর গণিত বাস্তব সংখ্যা

SSC (Class 9-10) Math । নবম দশম শ্রেণীর সাধারণ গণিত । অধ্যায় ১ বাস্তব সংখ্যা

1secondschoolLeave a comment
শেয়ার করুন

Table of Contents

বাস্তব সংখ্যাঃ স্বাভাবিক, ভগ্নাংশ, মূলদ, অমূলদ ও দশমিক সংখ্যাঃ

সংখ্যা (Number)

সংখ্যা (Number)

সংখ্যা হলো একটি বিমূর্ত ধারণা। সংখ্যা প্রকাশের প্রতীকগুলিকে বলা হয় অঙ্ক।

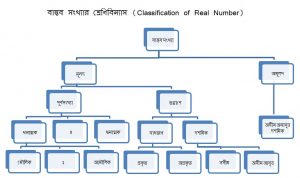
বাস্তব সংখ্যার শ্রেণিবিন্যাস (Classification of Real Number)

বাস্তব সংখ্যার শ্রেণিবিন্যাস করলে যে সকল সংখ্যা সম্পর্কে ধারণা লাভ করা যায় সেগুলো নিচে আলোচনা করা হল:

স্বাভাবিক সংখ্যা (Natural Number)

সকল ধনাত্মক অখন্ড সংখ্যা হল স্বাভাবিক সংখ্যা। যেমন:

1, 2, 3, 4, . . . . . .

মৌলিক সংখ্যা (Prime Number)

1 অপেক্ষা বড় যে সকল স্বাভাবিক সংখ্যার 1 এবং ঐ সংখ্যাটি ছাড়া আর কোনো গুণনীয়ক নেই সেকল সংখ্যাই মৌলিক সংখ্যা।  যেমন: 2, 3, 5, 7  ইত্যাদি। ক্ষুদ্রতম মৌলিক সংখ্যা হল 2 ।

1-100 পর্যন্ত সংখ্যাগুলোর মধ্যে মোট ২৫ টি মৌলিক সংখ্যা রয়েছে। ইরাটোস্থিনিস ছাঁকনির সাহায্যে এটি খুব সহজেই নির্ণয় করা যায়।

2, 3, 5 কেন মৌলিক সংখ্যা?

2, 3, 5 মৌলিক সংখ্যা। কারন:
2=1\times{2}
3=1\times{3}
5=1\times{5}

2, 3, 5  সংখ্যাগুলোর প্রতিটিরই 1 এবং ঐ সংখ্যা ছাড়া আর কোনো গুণনীয়ক নেই। তাই এই সংখ্যাগুলো মৌলিক সংখ্যা।

0 ও  1 ছাড়া সকল সংখ্যাই হয় মৌলিক সংখ্যা নয়তো যৌগিক সংখ্যা।

যৌগিক সংখ্যা

যে সংখ্যার দুইয়ের অধিক গুণনীয়ক আছে তাকে যৌগিক সংখ্যা বলে। যেমন 4, 6, 8, 21 ইত্যাদি যৌগিক সংখ্যা।

4, 6, 8, 21 কেন যৌগিক সংখ্যা?

4=1\times{4}=2\times{2} [4 এর গুণনীয়ক তিনটি 1, 2,4]

6=1\times{6}=2\times{3} [6 এর গুণনীয়ক চারটি 1, 2, 3, 6]

8=1\times{8}=2\times{4} [8 এর গুণনীয়ক চারটি 1, 2, 4, 8]

21=1\times{21}=3\times{7} [21 এর গুণনীয়ক চারটি 1, 3, 7, 21]

উল্লেখিত সংখ্যাগুলোর প্রত্যেকটিরই দুইয়ের অধিক গুণনীয়ক আছে। তাই সংখ্যাগুলো যৌগিক সংখ্যা।

1 মৌলিক সংখ্যাও নয় আবার যৌগিক সংখ্যাও নয়

1 মৌলিক সংখ্যা নয়। কারন:

1=1\times{1}

সকল মৌলিক সংখ্যার দুইটি ভিন্ন গুণনীয়ক থাকে। কিন্তু 1 এর গুণনীয়ক কেবলমাত্র একটি। 1 এর একমাত্র গুণনীয়কটি হল 1 । তাই 1 মৌলিক সংখ্যা হতে পারে না।

1 যৌগিক সংখ্যাও নয়। কারন:

সকল যৌগিক সংখ্যার দুইয়ের অধিক গুণনীয়ক থাকে। কিন্তু 1 এর গুণনীয়ক কেবলমাত্র একটি। তাই 1  যৌগিক সংখ্যা নয়।

পূর্ণসংখ্যা (Integer)

শূন্যসহ সকল ধনাত্মক ও ঋণাত্মক অখন্ড সংখ্যা হল পূর্ণসংখ্যা। যেমন:

. . . . . . . -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, . . . . . . . . . .

ভগ্নাংশ সংখ্যা (Fractional Number)

\frac{p}{q} আকারের সংখ্যাকে ভগ্নাংশ বলে। যেখানে, p, q পরস্পর সহমৌলিক। যেমন:

\frac{3}{5}, \frac{-2}{7}, \frac{11}{9} ইত্যাদি।

ভগ্নাংশগুলোর আবার শ্রেণি বিভাগ আছে। কিছু আছে প্রকৃত ভগ্নাংশ আবার কিছু আছে অপ্রকৃত ভগ্নাংশ।

প্রকৃত ভগ্নাংশ (Proper Fraction)

যে সকল ভগ্নাংশে লব হর অপেক্ষা ছোট সেগুলো প্রকৃত ভগ্নাংশ। যেমন:

\frac{3}{5}, \frac{-2}{7} ইত্যাদি।

অপ্রকৃত ভগ্নাংশ (Improper Fraction)

যে সকল ভগ্নাংশে লব হর অপেক্ষা বড় সেগুলো অপ্রকৃত ভগ্নাংশ। যেমন:

\frac{5}{3}, \frac{11}{7} ইত্যাদি।

মূলদ সংখ্যা (Rational Number)

\frac{p}{q} আকারের সকল সংখ্যাকে মূলদ সংখ্যা বলে, যেখানে, p, q পূর্ণসংখ্যা এবং q\ne{0} । যেমন:

3=\frac{3}{1}

\frac{3}{2}=1.5

\frac{11}{9}=1.222 . . . . . . . . ইত্যাদি।

সকল পূর্ণসংখ্যা এবং সকল ভগ্নাংশ মূলদ সংখ্যা।
মূলদ সংখ্যাকে দুইটি পূর্ণসংখ্যার অনুপাত হিসাবে প্রকাশ করা যায়।

অমূলদ সংখ্যা (Irrational Number)

যেসকল সংখ্যাকে \frac{p}{q} আকারে প্রকাশ করা যায় না, যেখানে, p, q পূর্ণসংখ্যা এবং q\ne{0} সেকল সংখ্যাকে অমূলদ সংখ্যা বলে। পূর্ণবর্গ নয় এরূপ যেকোনো স্বাভাবিক সংখ্যার বর্গমূল হল অমূলদ সংখ্যা। যেমন:

যেমন:

\sqrt{2}=1.41421356. . . . . . . ,

\sqrt{5}=2.236067. . . . . . .,

\sqrt{\frac{5}{2}}=1.58113 . . . . . . . . .  ইত্যাদি।
অমূলদ সংখ্যাকে দুইটি পূর্ণসংখ্যার অনুপাত হিসাবে প্রকাশ করা যায় না।

দশমিক ভগ্নাংশ সংখ্যা

মূলদ ও অমূলদ সংখ্যাকে দশমিকে প্রকাশ করা হলে তাকে দশমিক ভগ্নাংশ বলা হয়। যেমন:

5=5.0

\frac{7}{2}=3.5

\frac{5}{3}=1.6666. . . . . .

\sqrt{3}=1.732 . . . . . .  ইত্যাদ।

সসীম দশমিক ভগ্নাংশ

কোনো সংখ্যার দশমিক বিন্দুর পর অঙ্ক সংখ্যা সসীম হলে তাকে সসীম দশমিক ভগ্নাংশ বলে। যেমন:

5.25

3.527

1.5237 ইত্যাদি।

অসীম দশমিক ভগ্নাংশ

কোনো সংখ্যার দশমিক বিন্দুর পর অঙ্ক সংখ্যা অসীম হলে  অংশবিশেষ বারবার পূনরাবৃত্তি না হলে তাকে অসীম দশমিক ভগ্নাংশ বলে। যেমন:

\sqrt{2}= 1.414213562 . . . . . . . .

\sqrt{7}= 2.645751311 . . . . . . . . .

\sqrt{10}= 3.16227766 . . . . . . . . ইত্যাদি।

অসীম আবৃত্ত দশমিক ভগ্নাংশ বা পৌনঃপুনিক ভগ্নাংশ

কোনো অসীম দশমিক ভগ্নাংশের দশমিক বিন্দুর পর অঙ্কগুলো বা কিছু অঙ্ক পুনরাবৃত্তি হলে তাকে আবৃত্ত দশমিক ভগ্নাংশ বা অসীম আবৃত্ত দশমিক ভগ্নাংশ বা পৌনঃপুনিক ভগ্নাংশ বলে।  যেমন:

1.6666 . . . . . . . . .

2.53232323 . . . . . . . .

2.5\dot{3}\dot{2} ইত্যাদি।

উল্লেখ্য যে, অসীম দশমিক ভগ্নাংশের দশমিক বিন্দুর পর যে অংশটুকু পুনরাবৃত্তি ঘটে তাকে আবৃত্ত অংশ বলে। এই অংশটুকুর উপর পৌনঃপুনিক বিন্দু দিয়েও সংখ্যাটিকে প্রকাশ করা যায়। যেমন:

2.5323232 . . . . . . . . এর পরিবর্তে  2.5\dot{3}\dot{2},

7.245245245 . . . . . . . . এর পরিবর্তে  7.\dot{2}4\dot{5} লিখা যায়।

অসীম অনাবৃত্ত দশমিক ভগ্নাংশ

কোনো অসীম দশমিক ভগ্নাংশের দশমিক বিন্দুর পর অঙ্কগুলো পুনরাবৃত্তি না হলে তাকে অসীম অনাবৃত্ত দশমিক ভগ্নাংশ বলে। যেমন:

1.632405027 . . . . . . . .

1.737733777333 . . . . . . . . .

2.050055000555 . . . . . . . . ইত্যাদি।

ধনাত্মক সংখ্যা (Positive Number)

শূন্য অপেক্ষা বড় সকল বাস্তব সংখ্যাকে ধনাত্মক সংখ্যা বলে। যেমন:

1, 2, \frac{1}{2}, \frac{3}{2}, \sqrt{2}, 0.25, 0.\dot{5}\dot{7}, 4.12304605 . . . . , 1.3333 . . . . . ইত্যাদি।

ঋনাত্মক সংখ্যা (Negetive Number)

শূন্য অপেক্ষা ছোট সকল বাস্তব সংখ্যাকে ঋনাত্মক সংখ্যা বলে।  যেমন:

-1, -2, -\frac{1}{2}, -\frac{3}{2}, -\sqrt{2}, -0.25, -0.\dot{5}\dot{7}, -4.12304605 . . . . , -1.3333 . . . . . ইত্যাদি।

অঋনাত্মক সংখ্যা (Non-negetive Number)

শূন্যসহ সকল ধনাত্মক সংখ্যাকে অঋনাত্মক সংখ্যা বলে। যেমন:

0, 1, 2, \frac{1}{2}, \frac{3}{2}, \sqrt{2}, 0.25, 0.\dot{5}\dot{7}, 4.12304605 . . . . , 1.3333 . . . . . ইত্যাদি।

বাস্তব সংখ্যা (Real Number)

সকল মূলদ ও অমূলদ সংখ্যাই বাস্তব সংখ্যা। যেমন:

0,\pm{1}, \pm{2}, \pm{3},

\pm\frac{1}{2}, \pm\frac{3}{2}, \pm\frac{4}{3},

\sqrt{2}, \sqrt{3}, \sqrt{6},

2.75, 0.425, 1.3333 . . . . . . . . . ,

1.737733777333 . . . . . . . . . ,

2.5\dot{3}\dot{2} ইত্যাদি।

0 একটি কি সংখ্যা?

মজার বিষয় হলো, উত্তর ন্য(০) একটি স্বাভাবিক পূর্ণ সংখ্যা। ০ (উচ্চারণ: শূন্য) হলো একাধারে একটি সংখ্যা এবং অঙ্ক। এটি এককভাবে মানের অস্তিত্বহীনতা ও অন্যান্য সংখ্যার পিছনে বসে তাদের যুত পরিচয় প্রদান করে। এছাড়াও দশমিকের ডানে বসে এটি বিভিন্ন সংখ্যার দশমাংশ প্রকাশ করে।

অধ্যায় সমাধান

১. নিচের কোনটি অমূলদ সংখ্যা?

(ক) 0.3   (খ) √(16/9)   (গ) 3√ (8/27)   (ঘ) 5/√3
উত্তরঃ ঘ

২. a, b, c, d চারটি ক্রমিক স্বাভাবিক সংখ্যা হলে নিচের কোনটি পূর্ণবর্গ সংখ্যা?

(ক) abcd   (খ) ab+cd   (গ) abcd+1   (ঘ) abcd-1
উত্তরঃ গ

৩. 1 থেকে 10 পর্যন্ত মৌলিক সংখ্যা কয়টি?

(ক) 3   (খ) 4   (গ) 5   (ঘ) 6
উত্তরঃ খ

৪. কোনটি সকল পূর্নসংখ্যার সেট?

(ক) {…,-4, -2, 0, 2, 4, …}   (খ) {…, -2, -1, 0, 1, 2, …}
(গ) {…, -3, -1, 0,1, 3, …}     (ঘ) {0, 1, 2, 3, 4}
উত্তরঃ খ

৫. বাস্তব সংখ্যার ক্ষেত্রে

(i). বিজোড় সংখ্যার বর্গ একটি বিজোড় সংখ্যা।

(ii). দুইটি জোড় সংখ্যার গুণফল এর গুণিতিক জোড় সংখ্যা।
(iii). পূর্ণবর্গ নয় এমন সংখ্যার বর্গমূল মূলদ সংখ্যা।

নিচের কোনটি সঠিক?

(ক) i ও ii   (খ) i ও iii
(গ) ii ও iii   (ঘ) i, ii ও iii
উত্তরঃ ক

[ বি:দ্র: উত্তর দাতা ইসমাইল হোসেন ©সর্বস্বত্ব সংরক্ষিত (ওয়ান সেকেন্ড স্কুল )]

৬. তিনটি ক্রমিক স্বাভাবিক সংখ্যার গুণফল সর্বদাই নিচের কোন সংখ্যা দ্বারা বিভাজ্য হবে?

(ক) 5   (খ) 6   (গ) 7   (ঘ) 11
উত্তরঃ খ

৭. a ও b দুইটি ক্রমিক জোড় সংখ্যা হলে নিচের কোনটি বিজোড় সংখ্যা?

(ক) a2   (খ) b2   (গ) a2+1   (ঘ) b2+2
উত্তরঃ গ

৮. a ও b দুইটি পূর্ণসংখ্যা হলে a2+b2 এর সাথে নিচের কোনটি যোগ করলে যোগফল একটি পূর্ণবর্গ সংখ্যা হবে?

(ক) –ab   (খ) ab   (গ) 2ab   (ঘ) -2ab
উত্তরঃ গ

৯. প্রমান কর যে, প্রতিটি সংখ্যা অমূলদঃ (ক) √ 5   (খ) √ 7   (গ) √10

সমাধানঃ

(ক) √5
আমরা জানি,
1<5<9
বা, √1<√5<√9
বা, 1<√5<3
সুতরাং, √5   এর মান 1 অপেক্ষা বড় এবং 3 অপেক্ষা ছোট।
অতএব, √5   পূর্ণসংখ্যা নয়।
তাহলে, √5 মূলদ বা অমূলদ সংখ্যা হতে পারে।
যদি √5 মূলদ সংখ্যা হয় তবে,
মনে করি, √5=p/q [ যেখানে p ও q স্বাভাবিক সংখ্যা এবং q>1]
বা, 5=p2/q2 [বর্গ করে]
বা, 5q=p2/q [উভয় পক্ষকে q দ্বারা গুণ করে]
স্পষ্টতঃ 5q পূর্ণ সংখ্যা কিন্তু p2/q পূর্ণসংখ্যা নয়; কারন p ও q স্বাভাবিক সংখ্যা ও এরা পরস্পর সহমৌলিক এবং q>1.
তাহলে, 5q≠p2/q.
বা, 5≠p2/q2
বা, √5≠p/q
∴√5 একটি অমূলদ সংখ্যা।

(খ)√ 7  

আমরা জানি,
1<7<9
বা, √1<√7<√9
বা, 1<√7<3
সুতরাং, √7 এর মান 1 অপেক্ষা বড় এবং 3 অপেক্ষা ছোট।
অতএব, √7 পূর্ণসংখ্যা নয়।
তাহলে, √7 মূলদ বা অমূলদ সংখ্যা হতে পারে।
যদি √5 মূলদ সংখ্যা হয় তবে,
মনে করি, √7=p/q [ যেখানে p ও q স্বাভাবিক সংখ্যা এবং q>1]
বা, 7=p2/q2 [বর্গ করে]
বা, 7q=p2/q [উভয় পক্ষকে q দ্বারা গুণ করে]
স্পষ্টতঃ 7q পূর্ণ সংখ্যা কিন্তু p2/q পূর্ণসংখ্যা নয়; কারন p ও q স্বাভাবিক সংখ্যা ও এরা পরস্পর সহমৌলিক এবং q>1.
তাহলে, 7q≠p2/q.
বা, 7≠p2/q2
বা, √7≠p/q
∴√7 একটি অমূলদ সংখ্যা।

(গ)√ 10

আমরা জানি,
1<10<16
বা, √1<√10<√16
বা, 1<√10<4
সুতরাং, √10 এর মান 1 অপেক্ষা বড় এবং 4 অপেক্ষা ছোট।
অতএব, √10 পূর্ণসংখ্যা নয়।
তাহলে, √10 মূলদ বা অমূলদ সংখ্যা হতে পারে।
যদি √10 মূলদ সংখ্যা হয় তবে,
মনে করি, √10=p/q [ যেখানে p ও q স্বাভাবিক সংখ্যা এবং q>1]
বা, 7=p2/q2 [বর্গ করে]
বা, 10q=p2/q [উভয় পক্ষকে q দ্বারা গুণ করে]
স্পষ্টতঃ 10q পূর্ণ সংখ্যা কিন্তু p2/q পূর্ণসংখ্যা নয়; কারন p ও q স্বাভাবিক সংখ্যা ও এরা পরস্পর সহমৌলিক এবং q>1.
তাহলে, 10q≠p2/q.
বা, 10≠p2/q2
বা, √10≠p/q
∴√10 একটি অমূলদ সংখ্যা।

[ বি:দ্র: উত্তর দাতা ইসমাইল হোসেন ©সর্বস্বত্ব সংরক্ষিত (ওয়ান সেকেন্ড স্কুল )]

১০.

ক) 0.31 এবং 0.12 এর মধ্যে দুইটি অমূলদ সংখ্যা নির্ণয় কর।

সমাধানঃ

মনে করি,
একটি সংখ্যা a=0.301001000100001……………..
এবং অপর সংখ্যা b=0.302002000200002……….
স্পষ্টতঃ a ও b উভয়ই দুইটি বাস্তব সংখ্যা এবং উভয় 0.31 অপেক্ষা ছোট এবং 0.12 অপেক্ষা বড়।
অর্থাৎ, 0.31>0.3010010001………>0.12
এবং, 0.31>0.3020020002………..>0.12
আবার, a ও b কে ভগ্নাংশ আকারে প্রকাশ করা যায় না।
a ও b, 0.31 এবং 0.12 এর মাঝখানে অবস্থিত।
∴ a ও b দুইটি নির্ণেয় অমূলদ সংখ্যা।

খ) 1/√2 এবং √2 এর মধ্যে একটি মূলদ ও একটি অমূলদ সংখ্যা নির্ণয় কর।

সমাধানঃ

এখানে,
1/√2=0.707106
√2=1.4142
∴ 0.707106 ও 1.4142 এর মাঝখানে একটি মূলদ সংখ্যা a=0.70717071
∴ 0.707106 ও 1.4142 এর মাঝখানে একটি মূলদ সংখ্যা b=1.4141010010001……

১১.

ক) প্রমাণ কর যে, যেকোন বিজোড় পূর্ণসংখ্যার বর্গ একটি বিজোড় সংখ্যা।

সমাধানঃ

মনে করি, একটি বিজোড় সংখ্যা (2a-1)
∴ (2a-1)2
=(2a)2-2.2a.1+12
=4a2– 4a+1
=4a(a-1)+1
আমরা জানি,
যেকোনো পূর্ণসংখ্যাকে জোড় সংখ্যা দ্বারা গুণ করলে গুণফলও জোড় সংখ্যা হয়।
∴ 4a(a-1) একটি জোড় সংখ্যা [∴4 একটি জোড় সংখ্যা]
তাহলে, 4a(a-1)+1 একটি বিজোড় সংখ্যা।
∴ যেকোন বিজোড় পূর্ণসংখ্যার বর্গ একটি বিজোড় সংখ্যা।

খ) প্রমাণ কর যে, দুইটি ক্রমিক জোড় সংখ্যার গুণফল (আট) দ্বারা বিভাজ্য।

সমাধানঃ

মনে করি, দুইটি ক্রমিক সংখ্যা 2a ও 2a+2
তাহলে, 2a(2a+2)
=4a2+4a
=4a(a+1)
এখানে, a ও (a+1) দুইটি ক্রমিক সংখ্যা, সুতরাং এদের যে কোনো একটি অবশ্যই জোড় সংখ্যা হবে।
সুতরাং, a(a+1), 2 দ্বারা বিভাজ্য।
অতএব, 4a(a+1), 2✕4=8 দ্বারা বিভাজ্য।

১২. আবৃত দশমিক ভগ্নাংশে প্রকাশ কর।

(ক) 1/6
6) 10

6
40
36
40
36
40
36
4

 ( 0.16666…
    .

0.16 হলো নির্ণেয় আবৃত দশমিক ভগ্নাংশ।
(খ) 7/11
11) 70

66
40
33
70
66
40
33
70
66
4

 ( 0.63636…
      . .

0.63 হলো নির্ণেয় আবৃত দশমিক ভগ্নাংশ।
(গ) 2

3—

9
= 29

9
9) 29

27
20
18
20
18
20
18
2

 (3.222…
      .

3.2 হলো নির্ণেয় আবৃত দশমিক ভগ্নাংশ।
(ঘ) 8

3—

15
= 53

15
15) 53

45
80
75
50
45
50
45
50
45
5

 (3.5333…
    . .

3.53 হলো নির্ণেয় আবৃত দশমিক ভগ্নাংশ।

১৩. সাধারণ ভগ্নাংশে প্রকাশ করঃ

নবম শ্রেণীর গণিত বাস্তব সংখ্যা

১৪. সদৃশ আবৃত দশমিক ভগ্নাংশে প্রকাশ করঃ

(ক)    .

2.3,

      . .

5.235
এখানে, আবৃত দশমিকে অনাবৃত অংক

সংখ্যা সর্বোচ্চ 1 এবং আবৃত অঙ্ক সংখ্যা

1, 2 এর লসাগু=2.

∴ সদৃশ আবৃত দশমিক করতে হলে প্রত্যেক

দশমিকের পরে অনাবৃত অঙ্ক সংখ্যা হবে 1

এবং আবৃত অঙ্ক সংখ্যা হবে 2.
∴    .

2.3

        . .

=2.333

 [এরাই নির্ণেয়

সদৃশ

আবৃত দশমিক

ভগ্নাংশ]
     . .

5.235

        . .

=5.235
(খ)      .

7.26,

        .

4.237
এখানে, আবৃত দশমিকে অনাবৃত অংক

সংখ্যা সর্বোচ্চ 2 এবং আবৃত অঙ্ক সংখ্যা

1, 1 এর লসাগু=1.

∴ সদৃশ আবৃত দশমিক করতে হলে প্রত্যেক

দশমিকের পরে অনাবৃত অঙ্ক সংখ্যা হবে 2

এবং আবৃত অঙ্ক সংখ্যা হবে 1.
∴      .

7.26

          .

=7.266

 [এরাই নির্ণেয়

সদৃশ

আবৃত দশমিক

ভগ্নাংশ]
       .

4.237

          .

=4.237
(গ)      .

5.7,

    . .

8.34,

    .   .

6.245
এখানে, আবৃত দশমিকে অনাবৃত অংক

সংখ্যা সর্বোচ্চ 0 এবং আবৃত অঙ্ক সংখ্যা

1, 1, 3 এর লসাগু=6.

∴ সদৃশ আবৃত দশমিক করতে হলে প্রত্যেক

দশমিকের পরে অনাবৃত অঙ্ক সংখ্যা হবে 0

এবং আবৃত অঙ্ক সংখ্যা হবে 6.
∴    .

5.7

      .         .

=5.777777

 [এরাই

নির্ণেয়

সদৃশ

আবৃত

দশমিক

ভগ্নাংশ]
   . .

8.34

      .         .

=8.343434
   .     .

6.245

      .         .

=6.245245
(ঘ)  

12.32,

      .

2.19,

        . .

4.3256
এখানে, আবৃত দশমিকে অনাবৃত অংক

সংখ্যা সর্বোচ্চ 2 এবং আবৃত অঙ্ক সংখ্যা

0, 1, 2 এর লসাগু=2.

∴ সদৃশ আবৃত দশমিক করতে হলে প্রত্যেক

দশমিকের পরে অনাবৃত অঙ্ক সংখ্যা হবে 2

এবং আবৃত অঙ্ক সংখ্যা হবে 2.
∴ 12.32            . .

=12.3200

 [এরাই

নির্ণেয়

সদৃশ

আবৃত

দশমিক

ভগ্নাংশ]
     .

2.19

          . .

=2.1999
        . .

4.3256

          . .

=4.3256

১৫. যোগ করঃ

(ক)      .

0.45

 +        .

0.134
এখানে, অনাবৃত অংশের অঙ্ক সংখ্যা

সর্বোচ্চ 2 এবং আবৃত অংশের অংক

সংখ্যা 1.
সমাধানঃ
∴     .

0.45

 =        .

0.455
       .

0.134

 =        .

0.134
———————————
যোগফল        .

0.589
(খ)      .

2.05

 +      .

8.04

 + 7.018
সমাধানঃ
এখানে, অনাবৃত অংশের অঙ্ক সংখ্যা

সর্বোচ্চ 3 এবং আবৃত অংশের অংক

সংখ্যা 1.
∴      .

2.05

 =          .

2.0555
     .

8.04

 =          .

8.0444
7.018 =          .

7.0180
———————————
যোগফল            .

17.1179
(গ)        .

0.006

 +    . .

0.92

 +      .     .

0.0134
এখানে, অনাবৃত অংশের অঙ্ক সংখ্যা

সর্বোচ্চ 3 এবং আবৃত অংশের অংক

সংখ্যা 1, 2, 3 এর লসাগু 6.
∴        .

0.006

 =                . .

0.00666666
   . .

0.92

 =                . .

0.92929292
     .     .

0.0134

 =                 . .

0.01341341
—————————————
যোগফল                . .

0.94937299

১৬. বিয়োগ করঃ

(ক)    .

3.4

 –    .

2.13
সমাধানঃ
এখানে, অনাবৃত অংশের অঙ্ক সংখ্যা

সর্বোচ্চ 1 এবং আবৃত অংশের অংক

সংখ্যা 1.
∴    .

3.4

 =      .

3.44
     .

2.13

 =      .

2.13
—————————————–
বিয়োগফল      .

1.13
(খ)    . .

5.12

 –      .

3.45
সমাধানঃ      
এখানে, অনাবৃত অংশের অঙ্ক সংখ্যা

সর্বোচ্চ 1 এবং আবৃত অংশের অংক

সংখ্যা 1, 2 এর লসাগু 2.
∴    . .

5.12

 =      . .

5.121
     .

3.45

 =      . .

3.455
——————————————
     . .

1.666
=      -1
——————————————
বিয়োগফল      . .

1.665
(গ) 8.49 –      . .

5.356
সমাধানঃ      
এখানে, অনাবৃত অংশের অঙ্ক সংখ্যা

সর্বোচ্চ 2 এবং আবৃত অংশের অংক

সংখ্যা 2.
∴ 8.49 =        . .

8.4900
     . .

5.356

 =        . .

5.3565
———————————————
=        . .

3.1335
       -1
———————————————-
বিয়োগফল        . .

3.1334
(ঘ)          .

19.345

 –        .   .

13.2349
সমাধানঃ
এখানে, অনাবৃত অংশের অঙ্ক সংখ্যা

সর্বোচ্চ 2 এবং আবৃত অংশের অংক

সংখ্যা 1, 3 এর লসাগু 3.
∴          .

19.345

 =          .     .

19.34555
       .     .

13.2349

  =          .     .

13.23493
———————————————–
বিয়োগফল        .       .

6.11062

১৭. গুণ করঃ

ক) .

0.3

 ✕    .

0.6
সমাধানঃ
   .

0.3

 ✕    .

0.6
= 3

9

 ✕ 6

9
= 2

9
=    .

0.2
খ)    .

2.4

 ✕    . .

0.81
সমাধানঃ
   .

2.4

 ✕    . .

0.81
= 24-2

9

 ✕ 81

99
= 22

9

 ✕ 81

99
= 2
গ)      .

0.62

 ✕    .

0.3
সমাধানঃ
     .

0.62

 ✕    .

0.3
= 62-6

90

 ✕ 3

9
= 56

90

 ✕ 3

9
= 28

135
=      .     .

0.2074
ঘ)      .     .

42.18

 ✕      .

0.28
সমাধানঃ
    . .

42.18

 ✕      .

0.28
= 4218-42

99

 ✕ 28-2

90
= 4176

99

 ✕ 26

90
= 6032

495
=        .     .

12.185

১৮. ভাগ করঃ

ক)    .

0.3

 ÷    .

0.6
সমাধানঃ
   .

0.3

 ÷    .

0.6
= 3/9 ÷ 9/6
= 3/9 ✕ 6/9
= 1/2
= 0.5
খ)      .

0.35

 ÷    .

1.7
সমাধানঃ
     .

0.35

 ÷    .

1.7
= 35-3

90

 ✕ 17-1

9
= 32

90

 ✕ 9

1 9
= 1

5
= 0.2
গ)      .

2.37

 ÷      .

0.45
সমাধানঃ
      .

2.37

 ÷       .

0.45
= 237-13

90

 ÷ 45-4

90
= 214

90

 ÷ 41

90
= 214

90

 ✕ 90

41
= 214

41
=    .         .

5.21951
ঘ)    .    .

1.185

 ÷    . .

0.24
সমাধানঃ
   .     .

1.185

 ÷    . .

0.24
= 1185-1

999

 ÷ 24

99
= 1184

999

 ÷ 24

99
= 11894

999

 ✕ 99

24
= 1628

333
=    .

4.8

১৯. চার দশমিক স্থান পর্যন্ত বর্গমূল এবং তিন দশমিক স্থান পর্যন্ত সেগুলোর আসন্ন মান লেখঃ

বাস্তব সংখ্যা

২০. নিচের কোন সংখ্যাগুলো মূলদ এবং কোন সংখ্যাগুলো অমূলদ লিখঃ

 

(ক)    .

0.4
সমাধানঃ
   .

0.4
= 4

9
∴সংখ্যাটি মূলদ
(খ) √9
সমাধানঃ
√9
= √(3)2
= 3
∴সংখ্যাটি মূলদ
(গ) √11
সমাধানঃ
√11
= 3.31662…
∴সংখ্যাটি অমূলদ
(ঘ) √6

3
সমাধানঃ
√6

3
= √(3✕2)

3
= √3✕√2

3
= √2

√3
∴সংখ্যাটি অমূলদ
(ঙ) √8

√7
সমাধানঃ
= √8

√7
= √(2✕4)

√7
= 2√2

7
∴সংখ্যাটি অমূলদ
(চ) √27

√48
সমাধানঃ
√27

√48
= √(3✕9)

√(3✕16)
= √9

√3
= 3

4
∴সংখ্যাটি মূলদ
(ছ) 2

3

3

7
সমাধানঃ
2

3

3

7
= 2✕7

3✕3
14

9
   .

1.5
∴সংখ্যাটি মূলদ

২১. n=2x-1, যেখানে x ∈ N. দেখাও যে, n2 কে 8 (আট) দ্বারা ভাগ করলে প্রতিক্ষেত্রে 1 ভাগশেষ থাকবে।

সমাধানঃ

n=2x-1 [x ∈ N]
∴n2
=(2x-1)2
=(2x)2-2.2x+12
=4x2-4x+1
=4x(x-1)+1

x ∈ N বিধায়, x(x-1) জোড় সংখ্যা বা 4x(x-1) ও জোড় সংখ্যা আর 4x(x-1) কে 8 দ্বারা ভাগ করলে ভাগশেষ 0 হবে। তাহলে, 4x(x-1)+1 এর ক্ষেত্রে ভাগশেষ 1 হবে।
∴n=2x-1, যেখানে x ∈ N. দেখাও যে, n2 কে 8 (আট) দ্বারা ভাগ করলে প্রতিক্ষেত্রে 1 ভাগশেষ থাকবে।

২২. √5 ও 4 দুইটি বাস্তব সংখ্যা।

ক) কোনটি মূলদ ও কোনটি অমূলদ নির্দেশ কর।

খ) √5 ও 4 এর মধ্যে দুইটি অমূলদ সংখ্যা নির্ণয় কর।
গ) প্রমান কর যে, √5 একটি অমূলদ সংখ্যা।

সমাধানঃ

ক)
এখানে, √5=2.36067….
∴√5 একটি অমূলদ সংখ্যা
এবং 4 একটি মূলদ সংখ্যা।

খ)

এখানে, √5=2.36067….
মনে করি,
a=3.202002000….
b=3.505005000….
যেখানে, a ও b দুইটি বাস্তব সংখ্যা এবং √5 অপেক্ষা বড় ও 4 অপেক্ষা ছোট।
∴a ও b-ই নির্ণেয় দুইটি অমূলদ সংখ্যা।

গ)

৯(ক)-এর উত্তর দেখ।

২৩. সরল করঃ

Will be updated soon…

এতক্ষন আমাদের সাথে থাকার জন্য ধন্যবাদ!

আমাদের ইউটিউব চ্যানেলে সব সমাধান গুলো এখনি দেখে নাও!

Leave a Reply

Your email address will not be published. Required fields are marked *