বাস্তব সংখ্যা কি

বাস্তব সংখ্যা কি – অংক সমাধান সহ বিস্তারিত

1secondschoolLeave a comment
শেয়ার করুন

Table of Contents

বাস্তব সংখ্যা কি

বাস্তব সংখ্যা কি : বাস্তব সংখ্যার সজ্ঞা কয়েকভাবে দেয়া যায়। পরীক্ষায় আসলে অবশ্যই বইতে যে সজ্ঞা আছে তা দেবে। বইতে থাকা সজ্ঞাটি হলো “সকল মূলদ সংখ্যা এবং অমূলদ সংখ্যাকে মূলত বাস্তব সংখ্যা বলে।“
এখন এই সজ্ঞা বুঝতে হলে আমাদেরকে মূলদ এবং অমূলদ সংখ্যা সম্পর্কে বুঝতে হবে। আমরা মূলদ সংখ্যা এবং অমূলদ সংখ্যা সম্পর্কে একটু পরেই জানব, একই সাথে আগামী পর্বে আমরা এদেরকে নিয়ে আরেকটু বিস্তারিত জানার সাথে সাথে এদের মধ্যাকার পার্থক্য এবং মূলদ ও অমূলদ সংখ্যা চেনার উপায় সম্পর্কেও জানব। তবে মূলদ ও অমূলদ সংখ্যা চেনার আগেই তো আমাকে বাস্তব সংখ্যা চিনতে হবে। সেক্ষেত্রে সজ্ঞাটা হবে, “ধনাত্মক সংখ্যা, ঋণাত্মক সংখ্যা এবং শূন্যকে একত্রে বাস্তব সংখ্যা বলে।“

 What is Real number

আরও সহজ করে বলতে গেলে বলা যায় “প্রাত্যহিক জীবনে ব্যবহৃত সংখ্যাগুলোকেই বাস্তব সংখ্যা বলে।” বাস্তব সংখ্যার সেটকে R দ্বারা প্রকাশ করা হয় বলে এসএসসি লেভেলে পড়ানো হলেও আসলে একে প্রকাশ করা হয় R দ্বারা। উদাহারণস্বরূপ বলা যায়, 1, 2, -7, 3.1416…., 2.2222222222…, 52 ইত্যাদি সবই বাস্তব সংখ্যা।

বাস্তব সংখ্যার প্রকারভেদ

বাস্তব সংখ্যাকে ভাগ করতে চাইলে মূলত দুইভাগে ভাগ করা যায়।

  • মূলদ সংখ্যা
  • অমূলদ সংখ্যা

মূলদ সংখ্যাকে ২ ভাগে ভাগ করা যায়।

  • পূর্ণ সংখ্যা
  • ভগ্নাংশ

পূর্ণ সংখ্যাকে ৩ ভাগে ভাগ করা যায়।

  • ধনাত্মক পূর্ণসংখ্যা বা স্বাভাবিক সংখ্যা
  • শূন্য (০)
  • ঋণাত্মক সংখ্যা

ধনাত্মক পূর্ণ সংখ্যা আবার ৩ প্রকার।

 

  • মৌলিক সংখ্যা
  • এক (১)
  • যৌগিক সংখ্যা

অন্যদিকে আবার মূলদ সংখ্যার দ্বিতীয় ভাগ, অর্থাৎ ভগ্নাংশের প্রকার দুটি।

  • সাধারণ ভগ্নাংশ
  • দশমিক ভগ্নাংশ

সাধারণ ভগ্নাংশকে আবার দুই ভাগে ভাগ করা যায়।

  • প্রকৃত সাধারণ ভগ্নাংশ
  • অপ্রকৃত সাধারণ ভগ্নাংশ

অপ্রকৃত সাধারণ ভগ্নাংশের অধীনে আছে এক ধরনের ভগ্নাংশ। আর তা হচ্ছে,

  • মিশ্র ভগ্নাংশ

অন্যদিকে দশমিক ভগ্নাংশকে আবার দুইভাগে ভাগ করা যায়।

  • সসীম দশমিক ভগ্নাংশ
  • অসীম আবৃত্ত ভগ্নাংশ

আর একেবারে শুরুতে বাস্তব সংখ্যাকে যে দুইভাগ ভাগে করেছিলাম তার মধ্য থেকে দ্বিতীয় বিভাগটি অর্থাৎ অমূলদ ভগ্নাংশের একটি ভাগ আছে। আর তা হলো:

  • অসীম অনাবৃত্ত দশমিক

এবার আমরা এসবের বিস্তারিত জানার চেষ্টা করব। বাস্তব সংখ্যা কি 

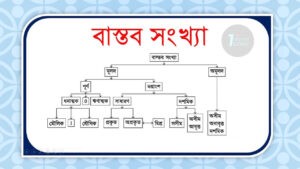
বাস্তব সংখ্যার প্রকারভেদ
বাস্তব সংখ্যা কি

বাস্তব সংখ্যাকে ভাগ করতে চাইলে মূলত দুইভাগে ভাগ করা যায়।

  • মূলদ সংখ্যা
  • অমূলদ সংখ্যা

মূলদ সংখ্যা (Rational Numbers):

𝑝/𝑞 আকারের যেকোনো সংখ্যাকে মূলদ সংখ্যা বলে, যখন p ও q পূর্ণসংখ্যা এবং q ≠ 0। যেকোনো মূলদ সংখ্যাকে দুইটি সহমৌলিক সংখ্যার অনুপাত হিসেবেও লেখা যায়। সকল পূর্ণসংখ্যা ও ভগ্নাংশই মূলদ সংখ্যা। যেমন 3/1 = 3, 11/2 = 5.5, 5/3 = 1.666 … সকল পূর্ণসংখ্যা ও ভগ্নাংশই মূলদ সংখ্যা।

মূলদ সংখ্যা চেনার উপায়

  • প্রত্যেক পূর্ণসংখা একটি মূলদ সংখ্যা।
  • সকল পূর্ণবর্গ সংখ্যার বর্গমূল মূলদ সংখ্যা। যেমন- √4, √9, √16।
  • সকল পূর্ণ ঘন সংখ্যার ঘনমূল মুলদ সংখ্যা। যেমন- ∛8, ∛27।
  • শূন্য, সকল স্বাভাবিক সংখ্যা, প্রকৃত ও অপ্রকৃত ভগ্নাংশ মূলদ সংখ্যা। যেমন- 0, 1, 2, 4, 5/12।
  • দশমিকের পরের ঘরগুলো সসীম হলে সেটি মূলদ সংখ্যা। যেমন- ৪.৫৬, ৬.৮৫ ইত্যাদি।
  • দশমিকের পরের ঘরগুলো অসীম এবং পৌন:পুনিক হলে। যেমন- 6.333….।

অমূলদ সংখ্যা (Irrational Number)

যেসকল সংখ্যাকে \frac{p}{q} আকারে প্রকাশ করা যায় না, যেখানে, p, q পূর্ণসংখ্যা এবং q\ne{0} সেকল সংখ্যাকে অমূলদ সংখ্যা বলে। পূর্ণবর্গ নয় এরূপ যেকোনো স্বাভাবিক সংখ্যার বর্গমূল হল অমূলদ সংখ্যা। যেমন:

যেমন:

\sqrt{2}=1.41421356. . . . . . . ,

\sqrt{5}=2.236067. . . . . . .,

\sqrt{\frac{5}{2}}=1.58113 . . . . . . . . .  ইত্যাদি।
অমূলদ সংখ্যাকে দুইটি পূর্ণসংখ্যার অনুপাত হিসাবে প্রকাশ করা যায় না।

অমূলদ সংখ্যা চেনার উপায়

১. যে সকল সংখ্যা পূর্ণবর্গ নয়। যেমন, √2, √3, √5।
২. দশমিক চিহ্নের পরের অঙ্কগুলো যদি পৌন:পুনিক না হয় এবং অসীম পর্যন্ত চলতে থাকে। যেমন- 6.6574…..।

মূলদ সংখ্যাকে ২ ভাগে ভাগ করা যায়।

  • পূর্ণ সংখ্যা
  • ভগ্নাংশ

পূর্ণসংখ্যা (Integer): শূন্যসহ সকল ধনাত্মক ও ঋণাত্মক অখন্ডক সংখ্যাকে পূর্ণসংখ্যা বলা হয়। অর্থাৎ -3 , -2 , -1 , 0 ,1 , 2, 3 ইত্যাদি পূর্ণসংখ্যা।

ভগ্নাংশ সংখ্যা (Fractional Numbers): 𝑝/𝑞 আকারে কোনো সংখ্যাকে সাধারণ ভগ্নাংশ বলে। যেখানে q ≠ 0 এবং q ≠ 1। যেমন 1/2, 3/2 ইত্যাদি সাধারণ ভগ্নাংশ। কোনো সাধারণ 𝑝/𝑞 ভগ্নাংশে p < q হলে প্রকৃত ভগ্নাংশ এবং p > q হলে অপ্রকৃত ভগ্নাংশ। যেমন: 5/13 প্রকৃত ভগ্নাংশ আবার 13/5 অপ্রকৃত ভগ্নাংশ।

 

পূর্ণ সংখ্যাকে ৩ ভাগে ভাগ করা যায়।

  • ধনাত্মক পূর্ণসংখ্যা বা স্বাভাবিক সংখ্যা
  • শূন্য (০)
  • ঋণাত্মক সংখ্যা

ধনাত্মক সংখ্যা (Positive Number)

শূন্য অপেক্ষা বড় সকল বাস্তব সংখ্যাকে ধনাত্মক সংখ্যা বলে। যেমন:

1, 2, \frac{1}{2}, \frac{3}{2}, \sqrt{2}, 0.25, 0.\dot{5}\dot{7}, 4.12304605 . . . . , 1.3333 . . . . . ইত্যাদি।

ঋনাত্মক সংখ্যা (Negetive Number)

শূন্য অপেক্ষা ছোট সকল বাস্তব সংখ্যাকে ঋনাত্মক সংখ্যা বলে।  যেমন:

-1, -2, -\frac{1}{2}, -\frac{3}{2}, -\sqrt{2}, -0.25, -0.\dot{5}\dot{7}, -4.12304605 . . . . , -1.3333 . . . . . ইত্যাদি।

0 একটি কি সংখ্যা

০ (উচ্চারণ: শূন্য) হলো একাধারে একটি সংখ্যা এবং অঙ্ক। শূন্য হলো একাধারে একটি সংখ্যা এবংঅঙ্ক। এটি এককভাবে মানের অস্তিত্বহীনতা ও অন্যান্য সংখ্যার পিছনে বসে তাদের যুক্ত পরিচয় প্রদান করে। এছাড়াও দশমিকের ডানে বসে এটি বিভিন্ন সংখ্যার দশমাংশ প্রকাশ করে। অঙ্ক হিসেবে ০ (শূন্য) একটি নিরপেক্ষ অংক এবং সংখ্যার স্থানধারক হিসেবে কাজ করে।।শূন্য(০) একটি স্বাভাবিক পূর্ণ সংখ্যা।

ধনাত্মক পূর্ণ সংখ্যা আবার ৩ প্রকার।

  • মৌলিক সংখ্যা
  • এক (১)
  • যৌগিক সংখ্যা

মৌলিক সংখ্যা (Prime Number)

1 অপেক্ষা বড় যে সকল স্বাভাবিক সংখ্যার 1 এবং ঐ সংখ্যাটি ছাড়া আর কোনো গুণনীয়ক নেই সেকল সংখ্যাই মৌলিক সংখ্যা।  যেমন: 2, 3, 5, 7  ইত্যাদি। ক্ষুদ্রতম মৌলিক সংখ্যা হল 2 ।

যৌগিক সংখ্যা

যে সংখ্যার দুইয়ের অধিক গুণনীয়ক আছে তাকে যৌগিক সংখ্যা বলে। যেমন 4, 6, 8, 21 ইত্যাদি যৌগিক সংখ্যা।

4, 6, 8, 21 কেন যৌগিক সংখ্যা?

4=1\times{4}=2\times{2} [4 এর গুণনীয়ক তিনটি 1, 2,4]

6=1\times{6}=2\times{3} [6 এর গুণনীয়ক চারটি 1, 2, 3, 6]

8=1\times{8}=2\times{4} [8 এর গুণনীয়ক চারটি 1, 2, 4, 8]

21=1\times{21}=3\times{7} [21 এর গুণনীয়ক চারটি 1, 3, 7, 21]

উল্লেখিত সংখ্যাগুলোর প্রত্যেকটিরই দুইয়ের অধিক গুণনীয়ক আছে। তাই সংখ্যাগুলো যৌগিক সংখ্যা।

অন্যদিকে আবার মূলদ সংখ্যার দ্বিতীয় ভাগ, অর্থাৎ ভগ্নাংশের প্রকার দুটি।

  • সাধারণ ভগ্নাংশ
  • দশমিক ভগ্নাংশ

সাধারণ ভগ্নাংশ

কোনো বস্তুকে নির্দিষ্ট ভাগে বিভক্ত করে তাকে হর দ্বারা এবং নির্দিষ্ট অংশ হতে গৃহীত অংশকে লব দ্বারা চিহ্নিত করে গাণিতিকভাবে প্রকাশ করলে তাকে সাধারণ ভগ্নাংশ বলে।

দশমিক ভগ্নাংশ সংখ্যা

মূলদ ও অমূলদ সংখ্যাকে দশমিকে প্রকাশ করা হলে তাকে দশমিক ভগ্নাংশ বলা হয়। যেমন:

5=5.0

\frac{7}{2}=3.5

\frac{5}{3}=1.6666. . . . . .

\sqrt{3}=1.732 . . . . . .  ইত্যাদ।

সসীম দশমিক ভগ্নাংশ

কোনো সংখ্যার দশমিক বিন্দুর পর অঙ্ক সংখ্যা সসীম হলে তাকে সসীম দশমিক ভগ্নাংশ বলে। যেমন:

5.25

3.527

1.5237 ইত্যাদি।

অসীম দশমিক ভগ্নাংশ

কোনো সংখ্যার দশমিক বিন্দুর পর অঙ্ক সংখ্যা অসীম হলে  অংশবিশেষ বারবার পূনরাবৃত্তি না হলে তাকে অসীম দশমিক ভগ্নাংশ বলে। যেমন:

\sqrt{2}= 1.414213562 . . . . . . . .

\sqrt{7}= 2.645751311 . . . . . . . . .

\sqrt{10}= 3.16227766 . . . . . . . . ইত্যাদি।

অসীম আবৃত্ত দশমিক ভগ্নাংশ বা পৌনঃপুনিক ভগ্নাংশ

কোনো অসীম দশমিক ভগ্নাংশের দশমিক বিন্দুর পর অঙ্কগুলো বা কিছু অঙ্ক পুনরাবৃত্তি হলে তাকে আবৃত্ত দশমিক ভগ্নাংশ বা অসীম আবৃত্ত দশমিক ভগ্নাংশ বা পৌনঃপুনিক ভগ্নাংশ বলে।  যেমন:

1.6666 . . . . . . . . .

2.53232323 . . . . . . . .

2.5\dot{3}\dot{2} ইত্যাদি।

উল্লেখ্য যে, অসীম দশমিক ভগ্নাংশের দশমিক বিন্দুর পর যে অংশটুকু পুনরাবৃত্তি ঘটে তাকে আবৃত্ত অংশ বলে। এই অংশটুকুর উপর পৌনঃপুনিক বিন্দু দিয়েও সংখ্যাটিকে প্রকাশ করা যায়। যেমন:

2.5323232 . . . . . . . . এর পরিবর্তে  2.5\dot{3}\dot{2},

7.245245245 . . . . . . . . এর পরিবর্তে  7.\dot{2}4\dot{5} লিখা যায়।

অসীম অনাবৃত্ত দশমিক ভগ্নাংশ

কোনো অসীম দশমিক ভগ্নাংশের দশমিক বিন্দুর পর অঙ্কগুলো পুনরাবৃত্তি না হলে তাকে অসীম অনাবৃত্ত দশমিক ভগ্নাংশ বলে। যেমন:

1.632405027 . . . . . . . .

1.737733777333 . . . . . . . . .

2.050055000555 . . . . . . . . ইত্যাদি।

সাধারণ ভগ্নাংশকে আবার দুই ভাগে ভাগ করা যায়।

  • প্রকৃত সাধারণ ভগ্নাংশ
  • অপ্রকৃত সাধারণ ভগ্নাংশ

প্রকৃত ভগ্নাংশ (Proper Fraction)

যে সকল ভগ্নাংশে লব হর অপেক্ষা ছোট সেগুলো প্রকৃত ভগ্নাংশ। যেমন:

\frac{3}{5}, \frac{-2}{7} ইত্যাদি।

অপ্রকৃত ভগ্নাংশ (Improper Fraction)

যে সকল ভগ্নাংশে লব হর অপেক্ষা বড় সেগুলো অপ্রকৃত ভগ্নাংশ। যেমন:

\frac{5}{3}, \frac{11}{7} ইত্যাদি।

বাস্তব সংখ্যা বিসিএস

EX-01.  একটি শ্রেণিতে যতজন ছাত্র-ছাত্রী আছে প্রত্যেকে তত পয়সার চেয়ে আরও 25 পয়সা বেশি করে চাঁদা দেওয়ায় মোট 75 টাকা উঠল । ঐ শ্রেণির ছাত্র-ছাত্রী সংখ্যা কত ?
সমাধানঃ
ধরি,
স্কুলে ছাত্র-ছাত্রী সংখ্যা = ক জন
১ জনে টাকা দিল = ক + ২৫ পঁয়সা
ক জনে টাকা দিল= ক ( ক+২৫) পঁয়সা
= ক^২ + ২৫ক পঁয়সা

প্রশ্নমতে,
ক^২ + ২৫ক = (৭৫ x ১০০)    |     (১ টাকা=১০০ পঁয়সা)
=>,ক^২ + ২৫ক -৭৫০০=০
বা,ক^২ +১০০ক-৭৫ক-৭৫০০ =০
=>,ক ( ক+১০০)-৭৫(ক+১০০)=০
(ক+১০০) (ক-৭৫)=০

এখন,                                          আবার,        
ক+১০০=০                                     ক – ৭৫ = 0                     
বা,ক= – ১০০ [গ্রহণযোগ্য­ নয়]         বা,ক =  ৭৫

সুতরাং ছাত্র-ছাত্রী সংখ্যা ৭৫ জন (Ans) বাস্তব সংখ্যা কি 


EX-02.  ২ টি সংখ্যার যোগফল ৪৮ এবং তাদের গুনফল ৪৩২ ।  তবে বড় সংখ্যাটি কত ?  

 

[পরিবার পরিকল্পনা অধিদপ্তর নিয়োগ পরীক্ষা , উপসহকারী কমিউনিটি মেডিকেল অফিসার- 2014]

A ৩৬*
B ৩৭
C ৩৮
D ৪০
Hint;  মনে করি,
সংখ্যা দুটি যথাক্রমে a ও b শর্তমতে,
a+b=48________(i)
ab=432________(ii)
(ii) হতে পাই,
b=432/a________(iii)
(iii) হতে b এর মান (i) তে বসিয়ে পাই, a+b=48
 432/a+a=48
=>, (432+a2)/a=48
বা, 432+a2=48a
=>, a2-48a+432=0
বা, a2-36a-12a+432=0
=>, a(a-36)-12(a-36)=0
বা, (a-12)(a-36)=0
∴ a=12,36
এখন,
a=12 হলে, b=432/12=36
a=36 হলে, b=432/36=12
∴ বড় সংখ্যাটি 36  (Ans)


EX-03.  ০.০৩× ০.০০৬× ০.০০৭ = ?

 (বিসিএস ৩৫তম)

A .০০০১২৬
B .০০০০০১২৬*
C .০০০১২৬০
D .১২৬০০০

Hint; দশমিকের পরে ২টি, ৩ টি এবং ৩টি অংক আছে প্রতিটি অংশে
গুণফলে দশমিকের পরে মোট (২+৩+৩)
= ৮টি অংক থাকবে
step-1:  ৩ × ৬ × ৭  =  ১২৬
step-2:   ০.  দশমিকের পরে ৮টি সংখ্যা হবে   ||   ০.০০০০০১২৬
Ans :  ০.০০০০০১২৬


EX-04.  পর পর ১০ টি সংখ্যার প্রথম ৫ টির যোগফল ৫৬০ হলে শেষ ৫ টির যোগফল কত ?
Hint;
ধরি,
প্রথম সংখ্যাটি = x
২য় সংখ্যাটি   =  x + ১
৩য় সংখ্যাটি  =  x + ২
৪্ র্থ  সংখ্যাটি =  x + ৩
৫ম সংখ্যাটি   =  x + ৪

প্রশ্নমতে ,
x + (x+ ১) + (x + ২) + (x +  ৩) + (x + ৪) = ৫৬০
বা, ৫x+১০= ৫৬০
=>, ৫x = ৫৫০
বা, x= ১১০
   ধরে নিতে হবে  – 
      শেষের প্রথম সংখ্যাটি = x + ৫
     শেষের ২য় সংখ্যাটি   =  x + ৬
     শেষের ৩য় সংখ্যাটি  =  x + ৭
     শেষের ৪্ র্থ  সংখ্যাটি =  x + ৮
     শেষের ৫ম সংখ্যাটি   =  x + ৯

.’. শেষ ৫ টি সংখ্যার যোগফল
   (x + ৫) + (x + ৬) + (x + ৭) + (x + ৮) + (x + ৯)  =  ­ ৫x + ৩৫
   = (৫×১১০) + ৩৫
   = ৫৮৫ (Ans)


EX-07. ৩ টি সংখ্যা গড় ৩৩ ।  দুটি সংখ্যা ২৪, ৪২ হলে ৩য় সংখ্যাটি কত  ?

খাদ্য অধিদপ্তর

Shortcut Solution:
২৪ + ৪২ + ৩য় সংখ্যা  /  ৩  =  ৩৩                      ||  ( / )  এই চিহ্ন টি ভাগের সংকেত প্রকাশ করে     
বা, ৬৬ + ৩য় সংখ্যা  =  ৯৯
  ৩য় সংখ্যা  =  ৯৯ – ৬৬
 . ‘ . ৩য় সংখ্যা =  ৩৩  (Ans)


EX-08.  যত – তত থাকলে  –
একটি সংখ্যা  ৯৯৯ থেকে যত ছোট ৭৯৭ থেকে তত বড়  । সংখ্যাটি কত  ?

বিসিএস

Hint;
সংখ্যা দুটির যোগ করে ২ দিয়ে ভাগ করলেই উত্তর  । (যত – তত) কথাটি থাকলে প্রতিবার একই ভাবে হবে ।
সমাধানঃ  ৯৯৯ + ৭৯৭ /  ২  =  ৮৯৮   (Ans) বাস্তব সংখ্যা কি 


EX-09.   ৩৬ সংখ্যাটির মোট কতগুলো ভাজক আছে  ?

বিসিএস

 Shortcut Solution:
 ৩৬ = ১ x ৩৬

        = ২ x  ১৮
        = ৩ x  ১২
        = ৪  x  ৯
        = ৬ x  ৬

EX-10.    একটি সংখ্যার অর্ধেক তার এক- ততীয়াংশের চেয়ে ১৭ বেশি,সংখ্যাটি কত ?


ক। ৫২
খ। ৮৪
গ। ১০২
ঘ। ২০৮
সমাধানঃ
ক এর মান যাচাই
৫২ এর অর্ধেক=৫২/২=২৬
৫২ এর এক-ততীয়াংশ=৫২/৩=১৭.৩৩
২৬-১৭.৩৩=৮.৬৭(১৭ হয় না)
কাজেই ক সঠিক নয়

খ এর মান যাচাই
৮৪ এর অর্ধেক=৮৪/২=৪২
৮৪ এর এক-ততীয়াংশ=৮৪/৩=২৮
৪২-২৮=১৪(১৭ হয় না)
কাজেই খ সঠিক নয়

গ এর মান যাচাই
১০২ এর অর্ধেক=১০২/২=৫১
১০২ এর এক-ততীয়াংশ=১০২/৩=৩৪
৫১-৩৪=১৭(প্রশ্নের ১৭ এর সাথে মিলে গেছে)
কাজেই গ সঠিক উওর

EX-11.    একটি সাভাবিক সংখ্যার বর্গের ৯ গুনের সাথে সংখ্যাটি যোগ করলে তা পরবর্তী স্বাভাবিক সংখ্যার সমান হয় ।
ক.৭

খ.৮

গ.৯

ঘ.১০
সমাধানঃ
ক এর মান যাচাই
১ম অংশ
৭ এর বর্গ=(৭)২=৪৯
সংখ্যাটির বর্গ+সংখ্যাটি=৪৯+৭
=৫৬
২য় অংশ
পরবর্তী স্বাভাবিক সংখ্যাটি=৭+১=৮
পরবর্তী স্বাভাবিক সংখ্যাটির ৯ গুন=৯*৮=৭২
১ম অংশ ও ২য় অংশ সমান নয়
কাজেই ক সঠিক নয়

খ এর মান যাচাই

১ম অংশ
৮ এর বর্গ=(৮)২=৬৪
সংখ্যাটির বর্গ+সংখ্যাটি=৬৪+৮
=৭২
২য় অংশ
পরবর্তী স্বাভাবিক সংখ্যাটি=৮+১=৯
পরবর্তী স্বাভাবিক সংখ্যাটির ৯ গুন=৯*৯=৮১
১ম অংশ ও ২য় অংশ সমান নয়
কাজেই খ সঠিক নয়

গ এর মান যাচাই
১ম অংশ
৯ এর বর্গ=(৯)২=৮১
সংখ্যাটির বর্গ+সংখ্যাটি=৮১+৯
=৯০
২য় অংশ
পরবর্তী স্বাভাবিক সংখ্যাটি=৯+১=১০
পরবর্তী স্বাভাবিক সংখ্যাটির ৯
গুন=৯*১০=৯০
১ম অংশ ও ২য় অংশ মিলে গেছে
কাজেই গ সঠিক উওর বাস্তব সংখ্যা কি 

EX-12.  কোন সংখ্যার ৪০% এর সাথে ৪২ যোগ করলে ফলাফল হবে সংখ্যাটির সমান ।(৩১ তম বিসিএস)

ক। ৭০

খ। ৮০

গ। ৯০

ঘ। ৭৫
সমাধানঃ
ক এর মান যাচাই
৭০ এর ৪০%=(৪০/১০০)*৭০
=২৮
সংখ্যাটির ৪০%+৪২
=২৮+৪২=৭০(সংখ্যাটির সমান)
ক সঠিক উওর

More….

১. যত দশমিক স্থান পর্যন্ত আসন্ন মান বের করতে হবে, এর পরবর্তী স্থানে 5, 6, 7, 8 বা 9 হলে শেষ স্থানটির সংখ্যার সাথে কত যোগ করতে হবে?
ক) 0
খ) 1
গ) 2
ঘ) কিছুই না
সঠিক উত্তর: (খ)

২. ধনাত্মক সংখ্যা কত অপেক্ষা বড়?
ক) -2
খ) 0
গ) 1
ঘ) 2
সঠিক উত্তর: (খ) বাস্তব সংখ্যা কি 

৩. নিচের তথ্যগুলো লক্ষ কর:
i. 7�0.3=5.4
ii. 1-0.5=4
iii. 1.3, 1.03 এবং 1.3 এর মধ্যে বৃহত্তম 1.3
নিচের কোনটি সঠিক?
ক) i ও ii
খ) i ও iii
গ) ii ও iii
ঘ) i, ii ও iii
সঠিক উত্তর: (গ)

৪. 8.269421…. সংখ্যাটির চার দশমিক স্থান পর্যন্ত মান কত?

ক) 8.2695
খ) 8.2694
গ) 8.269
ঘ) .8269
সঠিক উত্তর: (খ)

৫. 0.3� 0.6=কত?
ক) 1.8
খ) 1.18
গ) 0.2
ঘ) 0.02
সঠিক উত্তর: (গ)

৬. নিচের কোনটি অসীম আবৃত্ত দশমিক ভগ্নাংশ সংখ্যা?
ক) 1.234…
খ) 2.423
গ) 3.296…
ঘ) 5.6161…
সঠিক উত্তর: (ঘ)

৭. নিচের কোন ভগ্নাংশটিকে সসীম দশমিক ভগ্নাংশে প্রকাশ করা যায়?

ক) 1/3
খ) 3/11
গ) 7/17
ঘ) 627/100
সঠিক উত্তর: (ঘ)</p>

৮. a, b, c বাস্তব সংখ্যা হলে, a(b+c) = কি?

ক) ab+ac
খ) a+(b+c)
গ) a-(b+c)
ঘ) a(bc)
সঠিক উত্তর: (ক)

৯. 4� 0.125 এর সঠিক মান নিচের কোনটি?

ক) 0.64
খ) 6.4
গ) 3.2
ঘ) 32
সঠিক উত্তর: (ঘ)

১০. নিচের তথ্যগুলো লক্ষ কর:
i. প্রত্যেক পূর্ণসংখ্যাই মূলদ সংখ্যা
ii. স্বাভাবিক সংখ্যা সেটের বৃহত্তম সদস্য নেই
iii. দুইটি স্বাভাবিক সংখ্যার বিয়োগফল সর্বদা স্বাভাবিক সংখ্যা
নিচের কোনটি সঠিক?
ক) i ও ii
খ) i ও iii
গ) ii ও iii
ঘ) i, ii ও iii
সঠিক উত্তর: (ক)

১১. 0.7+0.8=কত?
ক) 1.3
খ) 2.5
গ) 1.5
ঘ) 1.6
সঠিক উত্তর: (ঘ)

১২. নিচের কোনগুরো যৌগিক সংখ্যা?
ক) -3, -2, -14, 0, 1, 2, 3
খ) 4, 6, 8, 9, 10
গ) 1, 3, 5, 7, 11
ঘ) 1, 2, 3, 4, 5
সঠিক উত্তর: (খ)

১৩. গণনাকারী সংখ্যার অপর নাম কী?
ক) মূলদ সংখ্যা
খ) অমূলদ সংখ্যা
গ) স্বাভাবিক সংখ্যা
ঘ) ঋণাত্মক সংখ্যা
সঠিক উত্তর: (গ)

১৪. 2.324, 7.213…, 10.239…, 7.2315 এর মধ্যে কোনগুলো সসীম দশমিক ভগ্নাংশ সংখ্যা?

ক) 2.324, 7.213….
খ) 7.213…., 10.239….
গ) 2.324, 7.2315
ঘ) 2.324, 10.239…., 7.2315
সঠিক উত্তর: (গ)

১৫. 4.3256893…. সংখ্যাটির চার দশমিক স্থান পর্যন্ত আসন্ন মান নিচের কোনটি?
ক) 4.3256
খ) .4325
গ) 4.3257
ঘ) 4.3266
সঠিক উত্তর: (গ)

১৬. পূর্ণবর্গ নয় এমন যেকোনো স্বাভাবিক সংখ্যার বর্গমূল কোন সংখ্যা?
ক) স্বাভাবিক সংখ্যা
খ) পূর্ণসংখ্যা
গ) মূলদ সংখ্যা
ঘ) অমূলদ সংখ্যা
সঠিক উত্তর: (ঘ)

১৭. নিচের তথ্যগুলো লক্ষ কর:
i. পূর্ণসংখ্যার সেটে ক্ষুদ্রতম সংখ্যা নেই
ii. পূর্ণসংখ্যঅর সেটে বৃহত্তম সংখ্যা নেই
iii. পূর্ণসংখ্যার সেটে যোগ, বিয়োগ এবং গুণ প্রক্রিয়ার ফল পূর্ণসংখ্যাই হয়
নিচের কোনটি সঠিক?
ক) i ও ii
খ) i ও iii
গ) ii ও iii
ঘ) i, ii ও iii
সঠিক উত্তর: (ঘ)

১৮. 3/5, 8/13, 15/23 ভগ্নাংশগুলো কোন ধরনের ভগ্নাংশ?

ক) প্রকৃত ভগ্নাংশ
খ) অপ্রকৃত ভগ্নাংশ
গ) মিশ্র ভগ্নাংশ
ঘ) কোনোটিই নয়
সঠিক উত্তর: (ক)

১৯. বিয়োগের ক্ষেত্রে পৌনঃপুনিক বিন্দু যেখানে শুরু সেখানে বিয়োজন সংখ্যা বিয়োজ্য সংখ্যা থেকে ছোট হলে সবসময় সর্ব ডানের অঙ্ক থেকে কত বিয়োগ করতে হয়?
ক) 0
খ) 1
গ) 2
ঘ) কোনটিই নয়
সঠিক উত্তর: (খ)

২০. 8/5, 5/6, 3/8, 12/5 ভগ্নাংশগুলোর মধ্যে কোনগুলো প্রকৃত ভগ্নাংশ?

ক) 8/5, 5/6
খ) 5/6, 3/8
গ) 8/5, 12/5
ঘ) 8/5, 3/8, 12/5
সঠিক উত্তর: (খ)

২১. 9.263, 2.4023, 18.613 সংখ্যাগুলো কোন ধরনের সংখ্যা?
ক) অসীম দশমিক ভগ্নাংশ সংখ্যা
খ) সসীম দশমিক ভগ্নাংশ সংখ্যা
গ) অসীম আবৃত্ত দশমিক ভগ্নাংশ সংখ্যা
ঘ) অসীম অনাবৃত্ত দশমিক ভগ্নাংশ সংখ্যা
সঠিক উত্তর: (খ)

২২. আবৃত্ত দশমিককে সব সময় কিসে পরিণত করা যায়?
ক) ভগ্নাংশে
খ) পূর্ণসংখ্যায়
গ) স্বাভাবিক সংখ্যায়
ঘ) কোনটিই নয়
সঠিক উত্তর: (ক)

২৩. যে অসীম দশমিক ভগ্নাংশ আবৃত্ত নয় তাকে কী বলে?
/>ক) মূলদ সংখ্যা
ss=”yoast-text-mark” />>খ) মৌলিক সংখ্যা
>গ) অমূলদ সংখ্যা
>ঘ) যৌগিক সংখ্যা
সঠিক উত্তর: (গ) <strong>বাস্তব সংখ্যা কি

২৪. কোন সংখ্যাকে দুইটি পূর্ণসংখ্যার অনুপাতে প্রকাশ করা যায় না?

ক) মূলদ সংখ্যা
খ) অমূলদ সংখ্যা<br />গ) পূর্ণসংখ্যা
ঘ) ভগ্নাংশ সংখ্যা<br />সঠিক উত্তর: (খ)

২৫. a বাস্তব সংখ্যা এবং a + (-a) = কি?
ক) 2a
খ) 0
গ) 1
ঘ) -2a
সঠিক উত্তর: (খ)

২৬. নিচের তথ্যগুলো লক্ষ কর:
i. 1.2 � 1.12=1.370
ii. 5.435 একটি বিশুদ্ধ আবৃত্ত দশমিক ভগ্নাংশ
iii. 4. ও 65 পরস্পর সহমৌলিক সংখ্যা
নিচের কোনটি সঠিক?
ক) i ও ii
খ) i ও iii
গ) ii ও iii
ঘ) i, ii ও iii
সঠিক উত্তর: (খ)

২৭. নিচের তথ্যগুলো লক্ষ কর:

i. কোনো ভগ্নাংশের লব ও হরকে স্বাভাবিক সংখ্যায় প্রকাশ করতে পারলে ঐ ভগ্নাংশটি একটি মূলদ সংখ্যা
ii. √7 একটি অমুলদ সংখ্যা
iii. আবৃত্ত দশমিক ভগ্নাংশ একটি অমূলদ সংখ্যা
নিচের কোনটি সঠিক?
ক) i ও ii
খ) i ও iii
গ) ii ও iii
ঘ) i, ii ও iii
সঠিক উত্তর: (ক)

২৮. i. শূন্য অপেক্ষা বড় সকল বাস্তব সংখ্যা ধনাত্মক সংখ্যা
ii. শূন্য অপেক্ষা ছোট সকল বাস্তব সংখ্যা ধনাত্মক সংখ্যা
iii. শূন্যসহ সকল ধনাত্মক সংখ্যা অঋণাত্মক সংখ্যা
নিচের কোনটি সঠিক?
ক) i ও ii
খ) ii ও iii
গ) i ও iii
ঘ) i, ii ও iii
সঠিক উত্তর: (গ)

২৯. সকল মূলদ ও অমূলদ সংখ্যার সেট নিয়ে নিচের কোনটি গঠিত হয়?
ক) বাস্তব সংখ্যার সেট
খ) স্বাভাবিক সংখ্যার সেট
গ) পূর্ণসংখ্যার সেট
ঘ) মৌলিক সংখ্যার সেট
সঠিক উত্তর: (ক)

৩০. 3.6, 2.65, 4.265 …. সংখ্যাগুলো কোন ধরনের সংখ্যা?

ক) স্বাভাবিক সংখ্যা
খ) ভগ্নাংশ সংখ্যা
গ) দশমিক ভগ্নাংশ সংখ্যা
ঘ) পূর্ণ সংখ্যা
সঠিক উত্তর: (গ)

৩১. নিচের কোনটি মৌলিক সংখ্যা?
ক) 18
খ) 48
গ) 23
ঘ) 9
সঠিক উত্তর: (গ)

৩২. নিচের তথ্যগুলো লক্ষ কর:

i. পূর্ণবর্গ সংখ্যা নয় বর্গমূল অমূলদ সংখ্যা
ii. আবৃত্ত দশমিকের গুণফল দশমিক হতেও পারে, নাও হতে পারে
iii. অমূলদ সংখ্যাকে মূলদ সংখ্যা দ্বারা গুণ করলে গুণফল অমূলদ সংখ্যা হয়
নিচের কোনটি সঠিক?
ক) i ও ii
খ) i ও ii
গ) ii ও iii
ঘ) i, ii ও iii
সঠিক উত্তর: (ঘ)

৩৩. নিচের কোনটি মূলদ সংখ্যা?

ক) √0.25
খ) √0.35<br />গ) √0.9
>ঘ) √0.10
সঠিক উত্তর: (ক)</p>

৩৪. নিচের তথ</p>

লো লক্ষ

কর: বাস্তব সংখ্যা কি 
i. পূর্ণবর্গ নয় এরূপ স্বাভাবিক সংখ্যার বর্গমূল নির্ণয় করলে মূলদ সংখ্যা পাওয়া যায়
ii. অমূলদ সংখ্যাকে দুইটি পূর্ণসংখ্যার অনুপাতরূপে দেখানো যায় না
iii. স্বাভাবিক সংখ্যার সেট অসীম সেট
নিচের কোনটি সঠিক?
ক) i ও ii
খ) i ও iii
গ) ii ও iii
ঘ) i, ii ও iii
সঠিক উত্তর: (গ)

৩৫. দশমিক ভগ্নাংশে দশমিক বিন্দুর পর অবৃত্তাংশ ছাড়া অন্য কোনো অঙ্ক না থাকলে, তাকে কি বলে?
ক) বিশুদ্ধ পৌনঃপুনিক
খ) অবিশুদ্ধ পৌনঃপুনিক
গ) মিশ্র পৌনঃপুনিক
ঘ) পূর্ণসংখ্যা
সঠিক উত্তর: (ক)

৩৬. কোনো ভগ্নাংশের লব ও হরকে স্বাভাবিক সংখ্যায় প্রকাশ করতে পারলে ঐ সংখ্যাটি কোন ধরনের সংখ্যা?
ক) অমূলদ সংখ্যা
খ) মূলদ সংখ্যা
গ) অসীম অনাবৃত্ত দশমিক ভগ্নাংশ সংখ্যা
ঘ) উপরের কোনটিই নয়
সঠিক উত্তর: (খ)

৩৭. √2 ও 4 এর ক্ষেত্রে নিচের কোনটি সঠিক?

ক) অসীম সংখ্যক মূলদ সংখ্যা আছে
খ) সসীম সংখ্যক মূলদ সংখ্যা আছে
গ) একটিমাত্র মূলদ সংখ্যা আছে
ঘ) কোনো অমূলদ সংখ্যা নেই
সঠিক উত্তর: (ক)

৩৮. মুলদ সংখ্যাকে দশমিকে প্রকাশ করলে নিচের কোনটি হবে?
ক) সসীম বা আবৃত্ত দশমিক ভগ্নাংশ হবে
খ) অসীম দশমিক হবে
গ) শুধু সসীম হবে
ঘ) অমূলদ সংখ্যা হবে
সঠিক উত্তর: (ক)

৩৯. শূন্যসহ সকল ধনাত্মক সংখ্যাকে কি বলা হয়?
ক) ঋণাত্মক সংখ্যা
খ) অঋণাত্মক সংখ্যা
গ) মূলদ সংখ্যা
ঘ) অমূলদ সংখ্যা
সঠিক উত্তর: (খ)

৪০. নিচের কোন ভগ্নাংশকে সসীম দশমিক ভগ্নাংশে প্রকাশ করা যায় না?
ক) 3/7
খ) 1/3
গ) 41/16
ঘ) 5/13
সঠিক উত্তর: (গ)

পরম মান নির্ণয়

যেকোনো একটি বাস্তব সংখ্যা x এর পরম মান ।x। প্রতীক দ্বারা প্রকাশ করা হয় এবং তার সংজ্ঞা নিম্নরূপে দেওয়া হল

।x। = x ,যখন x > 0

= 0 , যখন x = 0

= -x , যখন x < 0

প্রদত্ত সংজ্ঞা থেকে বোঝাযাচ্ছে ।x। এর মান কখনও ঋণাত্মক হতে পারেনা ।

উদাহরণস্বরূপ x = 2 হলে , ।x। = ।2। = 2

x = 0 , হলে |x| = |0| = 0

x = -2 , হলে |x| = |-2| = -(-2) = 2

সুতরাং কোনো বাস্তব সংখ্যার পরম মান বলতে তার সংখ্যমান ( Numerical value ) বোঝায় ।

পরম মানের বৈশিষ্ট্য (Properties of absolute values)

x , y যেকোনো দুটি বাস্তব সংখ্যা হলে ,

(i) ।x। = ।-x।

উদাহরণস্বরূপ , x = 2 হলে , |x| = |2| = 2 এবং |-x| = |-2| = 2

(ii) x≤|x|x≤|x| এবং −x≤|x|−x≤|x|

উদাহরণস্বরূপ , x = 2 হলে , |x| = |2| = 2 অতএব x = |x|

x = -2 হলে , |x| = |-2| = 2 অতএব x < |x|

(iii) ।x – y। = ।y – x।

প্রমাণ :- ।x – y। = ।-(y – x)। = ।y – x।

(iv) ।x – y। = ( x – y) , যখন x > y 

                = -( x – y) , যখন x < y 

(v) x = y হলে , ।x – y। = 0 হবে ; বিপরীতক্রমে , ।x – y। = 0 হলে , x = y হবে । 

আরও পড়ুন:

লাভ ও ক্ষতি বিভিন্ন পরীক্ষায় আসা প্রশ্নসহ সহজ সূত্রের মাধ্যমে সমাধান

(vi) |x+y|≤|x|+|y||x+y|≤|x|+|y|

প্রমাণ :- স্পষ্টতই , x≤|x|x≤|x| ; −x≤|x|−x≤|x| ; এবং y≤|y|y≤|y| ; −y≤|y|−y≤|y|

এখন , x+y≥0x+y≥0 হলে ,

|x+y|=x+y≤|x|+|y|...........(1)|x+y|=x+y≤|x|+|y|………..(i)

আবার , x + y < 0 হলে ,

|x+y|=−(x+y)=−x+(−y)≤|x|+|y|..........(2)|x+y|=−(x+y)=−x+(−y)≤|x|+|y|……….(ii)

সুতরাং (i) ও (ii) থেকে পাই , |x+y|≤|x|+|y||x+y|≤|x|+|y|

(vii) |x−y|≤|x|+|y||x−y|≤|x|+|y|

প্রমাণ :- |x−y|=|x+(−y)|≤|x|+|−y||x−y|=|x+(−y)|≤|x|+|−y| (iv) থেকে পাই ।

বা , |x−y|≤|x|+|y||x−y|≤|x|+|y|

(viii) |a±b|≤||a|−|b|=”mo”>||a±b|≤||a|−|b|| বাস্তব সংখ্যা কি 

 

প্রমাণ :- স্পষ্টতই , |a|≥|b||a|≥|b| হলে ,

|a|=|(a+b)−b|≤|a+b|+|b|⇒|a+b|≥|a|−|b|.......(1)|a|=|(a+b)−b|≤|a+b|+|b|⇒|a+b|≥|a|−|b|…….(i)

আবার , |b|≥|a||b|≥|a| হলে ,

|b|=|(a+b)−a|≤|a+b|+|a|⇒|a+b|≥|b|−|a|..........(2)|b|=|(a+b)−a|≤|a+b|+|a|⇒|a+b|≥|b|−|a|……….(ii)

সুতরাং (i) ও (ii) থেকে পাই

|a+b|≥||a|−|b|||a+b|≥||a|−|b||

একইভাবে  |a|≥|b||a|≥|b| হলে ,

|a|=|(a−b)+b|≤|a−b|+|b|⇒|a−b|≥|a|−|b|.......(3)|a|=|(a−b)+b|≤|a−b|+|b|⇒|a−b|≥|a|−|b|…….(iii)

আবার , |b|≥|a||b|≥|a| হলে ,

|b|=|(b−a)+a|≤|b−a|+|a|⇒|b−a|≥|b|−|a|..........(4)|b|=|(b−a)+a|≤|b−a|+|a|⇒|b−a|≥|b|−|a|……….(iv)

সুতরাং (iii) ও (iv) থেকে পাই ,

|a−b|≥||a|−|b|||a−b|≥||a|−|b||

(ix) |xy|=|x||y||xy|=|x||y|

 

প্রমাণ:-

প্রথমত , মনে করি x≥0,y≥0x≥0,y≥0  অতএব xy≥0xy≥0

এখন সংজ্ঞা থেকে পাই ।x। = x , ।y। = y এবং ।xy। = xy

অতএব ।xy। = ।x।।y।

দ্বিতীয়ত , x≥0,y<0x≥0,y<0 হলে , xy≤0xy≤0

সুতরাং সংজ্ঞা থেকে পাই ।x। = x , ।y। = – y এবং ।xy। = – xy

অতএব ।xy। = – xy = x .(-y) = ।x।।y।

একইভাবে x<0,y≥0x<0,y≥0 হলে , আমরা প্রমাণ করতে পারি ।xy। = ।x।।y।.

সুতরাং x এবং y এর সব বাস্তব মানে ।xy। = ।x।।y।.

(x) ∣∣xy∣∣=|x||y|(y≠0)|xy|=|x||y|(y≠0)

প্রমাণ :-

∣∣xy∣∣=∣∣x⋅1y∣∣=|x|⋅∣∣1y∣∣=|x|⋅1|y|=|x||y||xy|=|x⋅1y|=|x|⋅|1y|=|x|⋅1|y|=|x||y|

(xi) |x|≤y|x|≤y হলে , −y≤x≤y−y≤x≤y হবে । 

 

প্রমাণ :- মনে করি x≥0x≥0 তাহলে ।x। = x এবং −x≤x−x≤x

এখন |x|≤y|x|≤y হওয়ায় , x≤y⇒−x≥−yx≤y⇒−x≥−y

সুতরাং −y≤−x≤x≤y⇒−y≤x≤y−y≤−x≤x≤y⇒−y≤x≤y

আবার x≤0x≤0 হলে ।x। = -x এবং −x≥x−x≥x

এখন |x|≤y|x|≤y হওয়ায় , −x≤y⇒x≥−y−x≤y⇒x≥−y

সুতরাং −y≤x≤−x≤y⇒−y≤x≤y−y≤x≤−x≤y⇒−y≤x≤y

(xii) |x|≥y|x|≥y হলে x≥yx≥y অথবা x≤−yx≤−y হবে । 

প্রমাণ :- যদি x≥0x≥0 হয় তবে ।x। = x

তাহলে |x|≥y⇒x≥y|x|≥y⇒x≥y

আবার x≤0x≤0 হয় , তবে ।x। = -x

তাহলে

|x|≥y⇒−x≥y⇒x≤−y|x|≥y⇒−x≥y⇒x≤−y

(xiii) 0<|x−a|≤δ0<|x−a|≤δ হলে a−δ≤x≤a+δa−δ≤x≤a+δ হবে , যেখানে x≠ax≠a

প্রমাণ :- 0<|x−a|0<|x−a| থেকে বোঝাযায় , x≠ax≠a

আবার |x−a|≤δ|x−a|≤δ থেকে পাই , −δ≤x−a≤δ−δ≤x−a≤δ (xi) বৈশিষ্ট্য থেকে পাই।

−δ≤x−a≤δ⇒a−δ≤x−a+a≤a+δ⇒a−δ≤x≤a+δ−δ≤x−a≤δ⇒a−δ≤x−a+a≤a+δ⇒a−δ≤x≤a+δ

(xiv) |x−a|≥δ|x−a|≥δ হলে , x≥a+δx≥a+δ অথবা x≤a−δx≤a−δ হবে । 

(xv) |x−a|=b|x−a|=b হলে , x=a+bx=a+b অথবা x=a−bx=a−b</span> হবে । বাস্তব সংখ্যা কি 

সংক্ষিপ্তকরণ 

(1) 1 , 2 , 3 , 4 ,…………  সংখ্যসমূহকে স্বাভাবিক সংখ্যা বলা হয়। স্বাভাবিক সংখ্যার সেটকে N দ্বারা সূচিত করা হয় ; অর্থাৎ

N = { 1 , 2 , 3 , 4 , ………. }

(2) স্বাভাবিক সংখ্যসমূহের সঙ্গে – 1 , – 2 , – 3 , ………. এবং 0 (শূন্য) সংখ্যসমূহের সংযোজন করে যেসব সংখ্যা পাওয়া যায় তাদের পূর্ণসংখ্যা বা অখন্ড সংখ্যা বলে । পূর্ণসংখ্যার সেটকে I দ্বারা সূচিত করা হয় ।; অর্থাৎ

I={0,±1,±2,±3,..........}I={0,±1,±2,±3,……….}

(3) p ও q পরস্পর মৌলিক দুটি পূর্ণ হলে , pqpq আকারে প্রকাশিত সংখ্যাকে মূলদ সংখ্যা বলা হয় । এখানে q

(≠0)(≠0)

কে ধনাত্মক পূর্ণসংখ্যা এবং p কে ধনাত্মক বা ঋণাত্মক পূর্ণসংখ্যা বা শূন্য ধরা হয় । মূলদ সংখ্যার সেটকে Q দ্বারা সূচিত করা হয় । অর্থাৎ Q={pq:p∈I,q∈N}Q={pq:p∈I,q∈N}

(4) শূন্য দ্বারা ভাগ অসংজ্ঞাত ; অর্থাৎ a0a0 এর কোনো অর্থ নেই ।

(5) যেকোনো মূলদ সংখ্যাকে সসীম দশমিকে নাহলে আবৃত্ত দশমিকে প্রকাশ করা যায় এবং বিপরীতক্রমে তাও সত্য ।

(6) প্রত্যেক মূলদ সংখ্যাকে সংখ্যা – অক্ষের উপরে অবস্থিত একটি নির্দিষ্ট বিন্দু দ্বারা প্রকাশ করা যায় , কিন্তু এটি বিপরীতক্রমে সত্য নয় অর্থাৎ সংখ্যা অক্ষের উপরে অবস্থিত প্রত্যেক বিন্দু দ্বারা মূলদ সংখ্যা প্রকাশিত নাও হতে পারে ।

(7) যে সংখ্যাকে  pqpq আকারে প্রকাশ করা যায়না অথবা যে সংখ্যার দশমিক আকার অপৌনঃপুনিক ও অসীম তাকে অমূলদ সংখ্যা বলে ।

(8) সমস্ত মূলদ বা অমূলদ সংখ্যার সংকলন বা সমষ্টিকে বাস্তব সংখ্যা বলে। বাস্তব সংখ্যার সেটকে R দ্বারা সূচিত করা হয় ; অর্থাৎ

R = { x : x একটি মূলদ সংখ্যা বা অমূলদ সংখ্যা }

(9) সংখ্যা অক্ষের উপরে অবস্থিত এক একটি বিন্দু এক একটি বাস্তব সংখ্যাকে প্রকাশ করে ।

(10) বাস্তব সংখ্যা সর্বত্র নিবিড় এবং তাদের মধ্যে কোনো ফাঁক নেই ।

(11) মনে করি a ও b ( >a ) দুটি বাস্তব সংখ্যা এবং x তাদের মধ্যবর্তী যেকোনো একটি বাস্তব সংখ্যা। তাহলে (a , b) বা a < x < b কে a ও b সংখ্যা দুটির মুক্ত বিস্তার এবং [a , b] বা a≤x≤ba≤x≤b কে তাদের বদ্ধ বিস্তার বলে ।

(12) যেকোনো বাস্তব সংখ্যা x এর পরম মান ।x। প্রতীক দ্বারা প্রকাশ করা হয় ।

।x। = x ,যখন x > 0

= 0 , যখন x = 0

= -x , যখন x < 0

উদাহরণ 1. প্রমাণ করো যে 3–√3 মূলদ সংখ্যা নয় । 

সমাধান :- ধরি 3–√3 হল একটি মূলদ সংখ্যা। অতএব সংজ্ঞা অনুযায়ী আমরা লিখতে পারি pq=3–√pq=3 . যেখানে p হল একটি পূর্ণসংখ্যা বা অখন্ড সংখ্যা এবং q হল স্বাভাবিক সংখ্যা ।

তাহলে

(pq)2=3⇒p2q=3q(pq)2=3⇒p2q=3q

আমরা জানি যে p ও q পরস্পর মৌলিক । অতএব p2p2 এবং q পরস্পর মৌলিক পূর্ণসংখ্যা হবে । সুতরাং p2qp2q দ্বারা একটি মূলদ সংখ্যা প্রকাশিত হচ্ছে যা কোনো ধনাত্মক পূর্ণসংখ্যা নয় । অপর দিকে 3q দ্বারা একটি স্বাভাবিক সংখ্যা প্রকাশিত হচ্ছে । সুতরাং আমাদের কল্পনা সত্য নয় । অর্থাৎ 3–√3 একটি মূলদ সংখ্যা হতে পারে না ।

উদাহরণ 2. দেখাও যে বিজোড় স্বাভাবিক সংখ্যার বর্গকে 8 দ্বারা ভাগ করলে ভাগশেষ সর্বদা 1 হবে । 

সমাধান :- মনে করি একটি বিজোড় স্বাভাবিক সংখ্যা হল ( 2n + 1) যেখানে n হল যেকোনো স্বাভাবিক সংখ্যা . এখন এই বিজোড় স্বাভাবিক সংখ্যার বর্গকে 8 দ্বারা ভাগ করলে আমরা পাই

(2n+1)28=4n2+4n+18=4n(n+1)+18...........(i)(2n+1)28=4n2+4n+18=4n(n+1)+18………..(1)

আমরা জানি পরপর যেকোনো দুটি স্বাভাবিক সংখ্যার গুণফল একটি জোড় সংখ্যা হবে । অতএব আমরা মনে করতে পারি n(n +1) = 2m . (i) নং সমীকরণে এই মান বসিয়ে পাই 4×2m+18=8m+184×2m+18=8m+18 . ( 8m + 1 ) কে 8 দ্বারা ভাগ করলে ভাগশেষ সর্বদা 1 হবে ।

 

আমাদের পোষ্ট গুলো প্রতিনিয়ত আপডেট করা হয়। বিসিএস,প্রাইমারি সহ সব পরীক্ষার প্রতিনিয়ত প্রশ্ন অনুযায়ী পোষ্ট গুলো আমরা আপডেট করি। সবার জন্য শুভ কামনা রইলো।

এতক্ষন আমাদের সাথে থাকার জন্য ধন্যবাদ!

Leave a Reply

Your email address will not be published. Required fields are marked *