সূচক ও লগারিদম
সূচক ও লগারিদম: বড় বড় সংখ্যা বা অনেক ছোট সংখ্যা মনে রাখা কষ্টসাধ্য ব্যাপার। সূচকের মাধ্যমে এই ধরণের সংখ্যাগুলোকে সহজে প্রকাশ করা যায়। এতে করে গণনা করা বা সূচকের গাণিতিক সমস্যাগুলো সহজে সমাধান করা যায়। আবার সূচকের মাধ্যমেই যেকোনো সংখ্যার বৈজ্ঞানিক রুপ বা আদর্শ রুপ প্রকাশ করা যায়। সূচক থেকেই লগারিদমের সৃষ্টি হয়েছে। সংখ্যার বা রাশির গুন, ভাগ বা সূচক সম্পর্কিত সমস্যাগুলো লগারিদমের সাহায্যে সহজে করা যায়। যখন কম্পিউটার বা ক্যালকুলেটর আবিষ্কার হয়নি তখন এই লগারিদমের সাহায্যেই অনেক সমস্যা সমাধান করা হতো, যা এখনও মাঝে মাঝে ব্যবহার করা হয়।
সাধারণত সূচককে power বা শক্তি বলা হয়। যেমন: {a^n} এ n হলো a এর সূচক এবং এখানে a হচ্ছে ভিত্তি। দুটি রাশি গুণ আকারে থাকলে এবং তাদের ভিত্তি একই হলে তাদের power বা শক্তির যোগ হয়। যেমন: {a^m}×{a^n}={a^{m + n}}
লগারিদম কি
লগারিদম হচ্ছে পাওয়ারের বিপরীত তত্ত্ব। Logos এবং Arithmas নামক দুটি গ্রিক শব্দ হতে Logarithm শব্দটির উৎপত্তি। Logos অর্থ “আলোচনা” ও Arithmas অর্থ “সংখ্যা”। অর্থাৎ, Logarithm শব্দটির অর্থ “সংখ্যা বিষয়ক আলোচনা” গণিতশাস্ত্রে এটি হলে সূচকের বিপরীত প্রক্রিয়া। এর অর্থ হলো কোনো সংখ্যার এটা হলো সেই সূচক যেটাকে একটি নির্ধারিত মানের (ভিত্তি) ঘাত হিসাবে উন্নীত করলে প্রথমোক্ত সংখ্যাটি পাওয়া যায়। সহজভাবে, একটি সংখ্যাকে বার বার গুণ করলে, সংখ্যাটিকে যতবার গুণ করা হয়েছিল তা গণনা করে। যেমন: যেহেতু 1000 = 10 × 10 × 10 = 103 তাই 1000 এর দশ ভিত্তিক এটা হলো 3, অথবা log10 (1000) = 3। x এর b ভিত্তিক এটাকে বলা লেখা হয় logbx ।
লগারিদম
৭। Logb (mn) = Logb (m) + Logb (n)
৮। Logb (m/n) = Logb (m) – Logb (n)
৯। Logb (xy) = y logb (x)
১০। 
১১। m logb (x) + n logb (y) = logb ( xmy n )
১২। Logb (m + n) = Logb m + Logb (1 + n/m)
১৩। Logb (m – n) = Logb m + Logb (1 – n/m)
১৪। Lognm = logdm /logdn
সূচক বা ভিত্তি সংবলিত রাশিকে সূচক বলে। গণিতের ক্ষেত্রে এটি হলো সূচকের বিপরীত প্রক্রিয়া। এর অর্থ কোনো সংখ্যার এটি হলো সেই সূচক যেটাকে একটি নির্ধারিত মানের, (ভিত্তি) ঘাত হিসাবে উন্নীত করলে প্রথমোক্ত সংখ্যাটি পাওয়া যায়। সাধারণ ক্ষেত্রে এটা একটি সংখ্যা (ভিত্তি) কতবার গুণ করা হলো সেটা গণনা করে।
সূচক এর সূত্র
১। গুণ 
২। ভাগ 
৩। গুণফলের ঘাত 
৪। ভাগফলের ঘাত 
৫। ঘাতের ঘাত 
৬। ঋণাত্মক সূচক 
৭। শূন্য সূচক 
৮। 
হলে, 
যখন, 
৯। 
১০। 
১১। ![\sqrt[3]{a}= a^{\frac{1}{3}}](https://mathbd.com/wp-content/ql-cache/quicklatex.com-94a92b79cecbf58887b685e849c50767_l3.svg "Rendered by QuickLaTeX.com")
১২। ![\sqrt[n]{a}= a^{\frac{1}{n}}](https://mathbd.com/wp-content/ql-cache/quicklatex.com-4c56da3260008c35ae4ada77d9b95d59_l3.svg "Rendered by QuickLaTeX.com")
লগারিদমের সূত্র
১। 
২। 
৩। 
৪। 
৫। 
৬। 
হলে, 
৭। 
৮। 
৯। 
লগারিদম ও সূচকের সম্পর্ক
তাহলে সূচক ও লগারিদমের মধ্যে একটা ঘনিষ্ট সম্পর্ক আমরা দেখতে পাচ্ছি। এই সম্পর্কটিকে চিত্রের মাধ্যমে দেখে নিতে পারি:
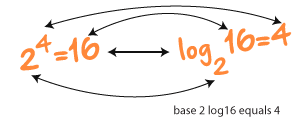চিত্রটিতে যে দুইটি বিষয় আমরা দেখতে পাচ্ছি তা আসলে একই জিনিসের দুইটি চেহারা ছাড়া আর কিছু নয়। এটাই হলো কথা যে, লগা সূচকীয় রাশির মান নির্ণয় করার জন্য ব্যবহার করা হয়। লগা সাহায্যে খুব সহজেই বড় বড় সংখ্যার গুণফল, ভাগফল ইত্যাদি নির্ণয় করা যায়।তাহলে, সূচকীয় রাশি আর লগামধ্যকার এই সম্পর্কের আরো কিছু উদাহরণ দেখি:
উল্লেখ্য যে, logarithm কে সংক্ষেপে log লেখা হয়।
সূচক ও লগারিদম সমাধান বিভিন্ন পরীক্ষায় আসা এমসিকিউ
1. 2log105 + log10 36 – log10 9 = ?
- 2
- 100
- 37
- 4.6
সঠিক উত্তরঃ 2
2.i49 এর মান কত?
- – 1
- i
- 1
- – i
সঠিক উত্তরঃ – i
3. যদি log10x = 1 হয়, তাহলে নিচের কোনটি x এর মান?
- 0.1
- 0.01
- 1/10000
- 0.001
সঠিক উত্তরঃ 0.1
4. কোন শর্তে a0 = 1 হয়?
- a = 0
- a সমান নয় 0
- a > 0
- a সমান নয় 1
সঠিক উত্তরঃ a সমান নয় 0
5. X-3 – 0.001=0 হলে x2 এর মান কত?
- 1
- কোনটিই নয়
- 10
- 100
সঠিক উত্তরঃ 100
7. 9x + 9x + 9x = কত?
- 27x +
- 32x-1 +
- 93x +
- 9x3 +
সঠিক উত্তরঃ 32x-1 +
8. 3-3 এর মান কত?
- 1/9
- 1/3
- 1/27
- 1/4
সঠিক উত্তরঃ 1/27